SISTEMA DE ECUACIONES NO LINEALES
ÍNDICE
1.- INTRODUCCIÓN
2.- MÉTODOS ITERATIVOS
3.- MÉTODOS CERRADOS
4.- MÉTODOS ABIERTOS
5.- BIBLIOGRAFÍA
Un sistema de ecuación es no lineal si, por lo menos, una de sus ecuaciones es no lineal (hay un grado mayor que uno.
Estos sistemas se resolverán habitualmente por sustitución. Es recomendable utilizar las ecuaciones del sistema en la medida de lo posible para hacer una idea aproximada de la situación de las soluciones, si las hay.
ejemplo

2.- MÉTODOS ITERATIVOS
Debe distinguirse entre el proceso iterativo completo y la formula de actualización
La verificación del término "satisfactorio" del proceso es esencial y debe anticipar para las posibles salidas del método iterativo.
Debe incluir test de validación de la consistente de datos.
3.- MÉTODOS CERRADOS
MÉTODO GRÁFICO
Los métodos gráficos consisten en graficar la función f(x) y observar donde la función cruza al eje x.
Pasos para su realización
- Para hacer este proceso más fácil es recomendable hacer una tabla con dos columnas, del lado izquierdo irá el valor a sustituir y del lado derecho irá el resultado del valor sustituido.
- Tomar una valor (puede ser cualquier número)
- Sustituir en la formula y anotar su resultado
- Identificar el resultado haciendo una gráfica (x - f(x))
- Unir tus anotaciones con lineas, por lo regular se anotan puntitos en la gráfica que al último se unen.
ejemplos:

- Para x = -4
y = (-4)^2 - 4 = 12
- Para x = -3.5
y = (-3.5)^2 - 4 = 8.3
- Para x = -3
y = (-3)^2 - 4 = 5
MÉTODO DE BISECCIÓN
Se trata de encontrar los ceros de f(x)=0, donde f es una función continua en [a,b] con f(a) y f(b) con signos diferentes.
De acuerdo con el teorema del valor medio, existe p ε [a,b] tal que f(p)=0.
El método cosiste en dividir a la mitad el intervalo y localizar la mitad que contiene a p.
El proceso se repite hasta lograrla precisión deseada.
El método de bisección se requiere de dos valores iniciales para ambos lados de la raíz, y que sus valores funcionales correspondientes sean de signos opuestos.
En este caso, el valor de XM se obtiene como el punto medio entre XI y XD.
XM = (XI + XD) / 2
Dependiendo de la función que se tenga en particular, el método de la bisección puede converger ligeramente más rápido o más lentamente.
En este método después de cada iteración el tamaño del intervalo se reduce a la mitad; después de n iteraciones, el intervalo original se habrá reducido 2^ n veces. Por lo anterior, si el intervalo origina es de tamaño a y el criterio de convergencia alicad al valor absoluto de la diferencia de dos XM consecutivas es ε, entonces se requerirán n iteraciones, donde n se calcula con la igualdad de la expresión.
(a / 2^ n) ≤ ε
De donde
n = (ln a - ln ε) / ln 2
Por eso se dice que se puede saber de antemano cuántas iteraciones se requieren.
Algoritmo
- f(x): Función a la cual se le busca la raíz.
- Elija valores iniciales inferior, Xl, y superior, Xu, que encierren la raíz, de tal forma que la función cambie de signo en el intervalo. Esto se verifica comprobando que f(Xl) f(Xu) ≤ 0.
- Una aproximación de la raíz x, se determina mediante: x=(Xl + Xu) /2
- Realice las sigueintes evaluaciones para determinar en qué subintervalo está la raíz.
A. Si f(Xl) f(Xu) ≤ 0, entonces la raíz se encuentra dentro del intervalo inferiror o
izquierdo. Por lo tanto, haga Xu =Xr y vuelve al paso 2.
B. Si f(Xl) f(Xu) ≤ 0, entonces la raíz se encuentra dentro del subintervalo superior o derecho. Por lo tanto, haga Xl =Xr y vuelve al paso 2.
C. Si f(Xl) f(Xu) = 0, la raiz es igual a Xr termina el cálculo.
ejemplo:
MÉTODO DE FALSA POSICIÓN
Este método pretende conjugar la seguridad del método de la bisección con la rapidez del método de la secante. Este método, como en el punto de bisección, parte de dos puntos que odean a la raiz f(x)=0, es decir, dos puntos X0 y X1 tales que f(X0)f(X1)<0. La siguiente aproximación, X2, se calcula como l intersección del eje X de la recta que une ambos puntos. La asignación del nuevo intervalo de búsqueda se realiza como en el método de la bisección entre ambos intervalos, [X0, X1] y [X2, X1], se toma aquel que cumpla f(x) f(X2)<0.
La elección guiada del intervalo representa una ventaja respecto al método de la secante ya que inhibe la posibilidad de una divergencia del método. Por otra parte y respecto al método de bisección , mejora notablemente la elección del intervalo.
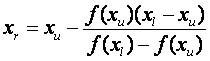
Esta es la fórmula de la falsa posición. El valor de Xr calculado con la ecuación reemplazará, después, a cualquiera de los dos valores iniciales, Xl o Xu, y da un valor de la función con el mismo signo de f(Xr). De esta manera, los valores Xl y Xu siempre encierran la verdadera raíz. El proceso se repite hasta que la aproximación a la raíz sea adecuada.
Algoritmo
- Elija valores iniciales inferior, Xi, y superior Xu, que encierran la raíz, de forma tal que la funciòn cambie de signo en el intervalo. Esto se verifica comprobando que f(xl) f(xu) <0.
- Una aproximación de la raíz xr se determina mediante:
3. Realice las siguientes evaluaciones para determinar en qué subintervalo está la raíz:
a) Si f(xl)f(xr) < 0, entonces la raíz se encuentra dentro del subintervalo inferior o izquierdo. Por lo tanto, haga xu = xr y vuelva al paso 2.b) Si f(xl)f(xr) > 0, entonces la raíz se encuentra dentro del subintervalo superior o derecho. Por lo tanto, haga xl = xr y vuelva al paso 2.c) Si f(xl)f(xr) = 0, la raíz es igual a xr; termina el cálculo.
ejemplo:
4.- MÉTODOS ABIERTOS
ITERACIÓN SIMPLE DE PUNTO FIJO
Es el método en el cual se utiliza una formula o expresión matemática para predecir la raíz, la misa que puede desarrollarse por una iteración simple, de allí su denominación.
Consiste en obtener na raíz, o solución, de una ecuación de la forma f(x)=0, la misma que debe ser transformada en una ecuación equivalente a un punto fijo g(x), de tal forma que al reordenar la ecuación f(x)=0, "x" se ubique al lado izquierdo de la ecuación de manera que se defina: x=g(x).
Método de iteración del punto fijo
- Básicamente, consiste en reordenar los términos de la función
- Se iguala a cero, para que la variable "x" quede a la izquierda
- x = g(x) ; x i+1 = g(x i)
Posteriormente, dado un valor inicial, para la raíz o al asignar una estimación inicial (xl), el punto fijo (x i) de "g", de tal forma que [x i punto fijo de g si x i=g(x i)]. x n+1=g(x n).
Entonces las ecuaciones anteriores pueden usarse para obtener una aproximación para k=1,2,3,... hasta que convergen, y expresada por a fórmula iteractiva x i+1 = g(x i) que generalizando se tiene: x i+1 = g(xn).
Resumen
- x = g(x)
- Tantear una raíz
- El valor de tanteo será el valor de inicio x0
- Una vez que se tiene x0, se evalúa g(x) en x0, denotándose el resultado de esta evaluación como x1; esto es g(x)= x1
- Caso 1: x1=x0, esto indica ue se ha elegido como valor inicial una raíz y el problema queda concluido
- Caso 2: que x1 ≠ x0, el cual es el caso más frecuent e indica que x1 y x0 son distintos, se procede a otra evaluación de g(x) ahora en x1, denotándose el resultado como x
MÉTODO DE NEWTON-RAPHSON
Es un método de segundo orden de convergencia cuando se trata de raíces reales no repetidas. Consiste en un procedimiento que lleva ecuación f(x) = 0 a la forma x=g(xi)=0, de modo que g'(x)=0.
La pendiente de la tangente a la curva en el punto (x0, f(x0)) es:
xi+1 = xi - (f(x) / f '(xi)) = g(xi)
Este método es de orden porque g'(x) = 0 y g''(xi) ≠ 0.
El objetivo de este método para estimar la solución de una ecuación f(x)=0 es producir una sucesión de aproximaciones que se acerquen a la solución (iteraciónes). Escogemos el primer número x0 de la secuencia y luego de circunstancias favorables el método hace el resto moviéndose paso a paso hacia la raíz.
Procedimiento del método
- Adivine una primera aproximación a la solución f(x) = 0. na gráfica de y = f(x) podría ayudarle a hacerlo.
- Use la primera aproximación para obtener la segunda, la segunda para obtener la tercera y asi sucesivamente usando la formula.
ejemplo:

MÉTODO DE LA SECANTE
Consiste en aproximar la derivada f '(x) de la ecuación xi+1 = xi - (f(x) / f '(xi)) = g(xi), por el cociente.
Teorema de Bolzano
Sea f:[a,b] -------> R, una función continua en [a,b] de forma que f distinto signo en los extremos, es decir: f(a)<0 y f(b)>0 o f(a)>0 y f(b)<0, entoces existe un valo c del intervalo (a, b) en el cual f(c)=0.
Fórmula de la secante
- xi+1 = x1 - [((x1-x0) f (x1)) / (f(x1) - f(x0))] = g(xi)
- Para la primera aplicación de la ecuación anterior e iniciar el proceso iterativo, se requerirán dos valores iniciales x0 y x1. La siguiente aproximación x está dada por:
x2 = x1 - [((x1-x0) f (x1)) / (f(x1) - f(x0))]
y así sucesivamente, hasta que xi+1 se acerque a 0.
ejemplo:
MÉTODO DE LAS RAÍCES MÚLTIPLES
Es conocido como el método de Newton-Raphson modificado.
Una de las condiciones para garantizar la convergencia del método de Newton-Raphson es que f ' (P) ≠ 0 donde P es la raíz de la ecuación f(x)=0. Si al momento de ejecutar el método de Newton-Raphson se observa que f ' (P) se aproxima a 0 (cero), se nota que la rapidez de convergencia del método disminuye. Del mismo modo se entiende que si en un valor de P se presenta simultáneamente que f (P) y f ' (P) que , entonces P es un valor crítico de x.
Se dice que P es una raíz de multiplicidad m de f si f(x) puede escribirse: f(x)=(x-P)^m q(x), donde q(P) ≠ 0 Si m = 1 , se llama raíz simple.
Paso a paso:
a) Elegir un punto inicial cualquiera x1 como aproximación de la raíz.
b) Obtener los valores de la función, de su primera y de su segunda derivada en ese punto.
c) Establecer la función u(x)= f(x) / f ' (x) y obtener el valor de la misma en el punto inicial.
d) Trazar una recta tangente a la función u(x) por ese punto.
e) El punto de intersección de esta recta con el eje de las abscisas (x2, 0), constituye una segunda aproximación de la raíz.
f) El proceso se repite n veces hasta que el punto de intersección xn coincide prácticamente con el valor exacto de la raíz.
Se utiliza la siguiente ecuación para hallar el intercepto con el eje x:







No hay comentarios:
Publicar un comentario