INDICE
1.- Introducción
a los métodos numéricos
2.- Definición
de los métodos numéricos
2.1.- Aproximación y errores
2.1.1.- Exactitud
2.1.2.- Precisión
2.1.3.- Incertidumbre
2.1.4.- Serie de Taylor
2.1.5.- Sesgo
2.1.6. Cifras Significativas
2.1.7.- Notación científica
2.1.8.- Modelos matemáticos
3.- Conceptos básicos
3.1.- Algoritmos
3.2.- Aproximaciones
4.- Tipos de errores
4.1.- Error
4.2.- Error de redondeo
4.3.- Error de truncamiento
4.4.- Errores absoluto
4.5.- Error relativo
4.6.- Error porcentual
5.- Convergencia
6.- Programas computacionales
6.1.-Octave
6.2.- Patran
6.3.- Integralab
6.4.- Elmer
6.5.- Octave
7.- Conclusión
8.- Bibliografía
1.- INTRODUCCIÓN A LOS MÉTODOS
NUMÉRICOS
Los métodos numéricos son técnicas mediante las cuales es posible
formular problemas matemáticos de tal forma que puedan resolverse usando
operaciones aritméticas.
Los métodos numéricos nos vuelven aptos para entender esquemas numéricos
a fin de resolver problemas matemáticos, de ingeniería y científicos en una
computadora, reducir esquemas numéricos básicos, escribir programa y resolver
en una computadora, usar correctamente el software para dichos métodos entre
otras cosas.
Al momento de aplicar las Matemáticas a situaciones del mundo real nos
encontramos a menudo con problemas que no pueden ser resueltos analíticamente o
de manera exacta y cuya solución debe ser abordada con ayuda de algún
procedimiento numérico. A continuación consideramos algunos problemas típicos,
ya formulados matemáticamente, para los cuales estudiaremos técnicas numéricas
de solución.
2.- DEFINICIÓN DE MÉTODOS NUMÉRICOS
Un método numérico es un
procedimiento mediante el cual se obtiene, casi siempre de manera aproximada,
la solución de ciertos problemas realizando cálculos puramente aritméticos y
lógicos (operaciones aritméticas elementales, cálculo de funciones, consulta de
una tabla de valores, cálculo preposicional, etc.).
Este procedimiento
consiste en una lista finita de instrucciones precisas que especifican una secuencia
de operaciones algebraicas y lógicas (algoritmos).
Son metodologías que utilizan técnicas algebraicas y aritméticas que se realizan a
partir de un problema planteado para resolver de forma aproximada ecuaciones o sistemas de ecuaciones complejas, que analíticamente
resultan muy difíciles de resolver, las cuales es posible formular problemas con operaciones aritméticas. En si es una herramienta matemática que ahora gracias a lo avanzado de la programación (calculadoras), ayudan a resolver problemas
de iteración y matemáticos.
2.1 APROXIMACIÓN Y ERRORES
Por truncamiento: generado
por usar una aproximación en lugar de un procedimiento exacto.
2.1.1.- Exactitud
Refiere a la precisión de algo, al ajuste de una cosa con otra, o a la
veracidad que ostenta una cuestión. En términos estadísticos, la exactitud
está relacionada con el sesgo de una estimación. Cuanto menor es el
sesgo más exacto es una estimación.
2.1.2.- Precisión
Es la necesidad y obligación de exactitud y concisión a la hora de
ejecutar algo, e este sentido, es la dispersión del conjunto de valores de una
magnitud: a menos dispersión, mayor precisión.
2.1.3.- Incertidumbre
Se denomina a la situación de desconocimiento que se tiene acerca de los
que sucederá en el futuro. Es como una Probabilidad de que un resultado esté fuera de la cota establecida o
de un gran margen de error sin certeza.
2.1.4.- Serie de Taylor
Suponga que f(x) es una función, y que todas las derivadas f', f'', f''', existen en x = a. Entonces la serie de Taylor de f(x) es la serie de potencias. Es
una representación o una aproximación de una función como una suma de términos
calculados de los valores de sus derivadas en un mismo punto.
Ejemplo:
2.1.5.- Sesgo
Es un alejamiento sistemático del valor verdadero a calcular. Así como
el error, de acuerdo con las formas por las cuales se produce, puede
minimizarse, la ocurrencia del sesgo puede ser neutralizada o controlada.
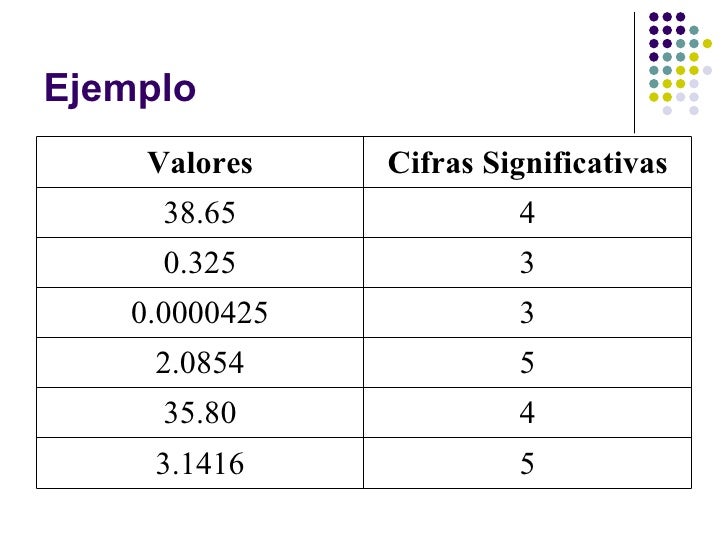
2.1.6.- Cifras Significativas
Se define como aquella que aporta información no ambigua ni superflua
acerca de una determinada medida experimental.
El concepto de cifras significativas tiene dos implicaciones importantes
el estudio de los métodos numéricos:
1.
Los métodos numéricos obtienen resultados próximos. Por lo tanto, se beben
desarrollar criterios para especificar qué tan precisos son los resultados
obtenidos.
2.
Aunque ciertos números presentan números específicos no se pueden
expresar exactamente con un número finito.
2.1.7.- Notación Científica
La notación científica nos permite escribir números muy grandes o muy
pequeños de forma abreviada. Esta notación consiste simplemente en multiplicar
por una potencia de base 10 con exponente positivo o negativo
Ejemplo
2 * 10^2 = 200
5769 = 5.769 * 10^3
Potencia 10 exponente positivo
Si n es positivo, la potencia de base 10 con
exponente n, es decir, 10^n, es el número formado
por la cifra 1 seguida de n ceros.
Ejemplo
10^1 = 10
10^2 =
100
10^3 =
1000
Potencia 10 exponente negativo
La potencia de base 10 con exponente negativo -n, es
decir, 10^-n, es el número decimal 0,00...01 siendo n el
número total de ceros.
Ejemplo:
0.00536 = 5.36 * 10^-3
2.1.8.- Modelos
Matemáticos
Un modelo matemático se define como una descripción desde el punto de
vista de las matemáticas de un hecho o fenómeno del mundo real, desde el tamaño
de la población, hasta fenómenos físicos como la velocidad, aceleración o
densidad. El objetivo del modelo matemático es entender ampliamente el fenómeno
el fenómeno y tal vez predecir su comportamiento en el futuro.
El proceso para elaborar un modelo matemático es el siguiente:
1.
Encontrar un problema del mundo real.
2.
Formular un modelo matemático acerca del problema, identificando
variables (dependientes e independientes) y estableciendo hipótesis lo
suficiente simples para tratarse de manera matemática.
3.
Aplicar los conocimientos matemáticos que se posee para llegar a
conclusiones matemáticas.
4.
Comparar los datos obtenidos como predecir con datos reales. Si los
datos son diferentes, se reinicia el proceso.
Es importante mencionar que el modelo matemático no es completamente
exacto con problemas de la vida real, se trata de una idealización.
Si los métodos numéricos sirven para resolver problemas de ingeniería
civil, se debe crear un modelo matemático que represente al sistema real.
Los modelos matemáticos generalmente se presentan con funciones donde
una variable depende de parámetros y otras variables independientes. Si el
modelo matemático es adecuado, podemos predecir el comportamiento del sistema
real.
Por naturaleza, los métodos numéricos producen soluciones aproximadas a
los problemas matemáticos pero pueden ser muy útiles para caracterizar un
sistema real.
3.- CONCEPTOS BÁSICOS
3.1.- Algoritmo
Un algoritmo es un método para resolver un problema paso a paso.
Los pasos para la resolución de algoritmo son:
1. Diseño de algoritmo: describe
la secuencia ordenada de pasos, sin ambigüedades, que conducen a la solución de
un problema dado (análisis del problema y desarrollo del algoritmo).
2. Expresar el algoritmo
como un programa en lenguaje de programación adecuado.
3. Ejecución y
validación del programa por computadora.
Las características fundamentales que debe cumplir todo algoritmo son:
- Un
algoritmo debe ser preciso e indicar el orden de realización de cada paso.
- un
algoritmo debe estar definido. Si se sigue un algoritmo dos veces, se debe
obtener el mismo resultado cada vez.
- Un
algoritmo debe ser finito. Si se sigue un algoritmo, se debe terminar en
algún momento; o sea, debe tener un número finito de pasos.
Los métodos usuales para representar un algoritmo son:
1.
Diagrama de flujo
2.
Diagrama N-S
3.
Lenguaje de especificación de algoritmo: pseudocódigo
4.
Lenguaje español, inglés
5.
Fórmulas
Diagrama de flujo
Es una técnica de programación de representación de algoritmos antigua y
muy utilizada. Se define como un diagrama que utiliza símbolos (cajas) y que
tiene los pasos de un algoritmo escrito en cajas unidas por flechas,
denominadas líneas de flujo, que indica la secuencia que se deben ejecutar.
Programa
Un programa de una computadora es el conjunto de instrucciones
(ordenadas a la máquina) que producirán la ejecución de una determinada tarea.
En esencia, un programa es un medio para conseguir un fin. El fin será
normalmente definido como la información necesaria para solucionar un problema.
3.2.- Aproximaciones
La mayor parte de las técnicas tiene la característica de poseer
errores. El concepto de aproximación suele emplearse para nombrar a la
obtención de un resultado que, si bien no es exacto, resulta próximo a la
exactitud.
En el terreno de las matemáticas, una aproximación es una representación
que, si bien no es exacta, se considera útil gracias a su fidelidad a la
realidad.
En algunos conceptos básicos de aproximaciones podemos encontrar:
- Cifras
significativas
- Precisión
- Exactitud
- Incertidumbre
- Sesgo
4.- TIPOS DE ERRORES
4.1.- Error
Surgen del uso de aproximaciones para representar
operaciones y cantidades exactas
4.2.- Error de redondeo
Producido
por no utilizar el valor real de un número en los cálculos.
Las siguientes reglas dan la pauta a seguir
en el redondeo de números cuando se realizan cálculos a mano.
1. En el redondeo, se conservan las cifras significativas y el resto se
descarta. El último dígito que se conserva se aumenta en uno si el primer
dígito descartado es mayor de 5. De otra manera se deja igual. Si el primer
digito descartado es 5 o es 5 segundo de ceros, entonces el último dígito
retenido se incrementa en 1, sólo si es impar.
2. En la suma y en la resta, el redondeo se lleva acabo de forma tal que
el último dígito en la columna de las milésimas.
3. Para la multiplicación y para la división el redondeo es tal que la
cantidad de cifras significativas del resultado es igual al número más pequeño
de cifras significativas que contiene la cantidad en la operación.
4. Para combinaciones de las operaciones aritméticas, existen dos casos
generales. Se puede sumar o restar el resultado o de las divisiones o también
se pueden multiplicar o dividir los resultados de las sumas y las restas.
Ejemplo:
p = 3.14159265… = 3.1416
e = 2.718281824… = 2.7183
4.3.- Error de truncamiento
Cuando una expresión
matemática se remplaza por una fórmula más simple, se introduce un error,
conocido como error de truncamiento.
Los errores de truncamiento
son aquellos que resultan al usar una aproximación en lugar de un procedimiento
matemático exacto.
Ejemplo:
p = 3.14159265… = 3.141
e = 2.718281824… = 2.718
4.4.- Error absoluto
Es la diferencia entre el
valor de la medida y el valor tomado como exacto. Puede ser positivo o
negativo, según si la medida es superior al valor real o inferior (la resta
sale positiva o negativa). Tiene unidades, las mismas que las de la
medida.
El error absoluto de una
medida no nos informa por sí solo de la bondad de la misma. Es evidente, que no
es igual de grave tener un error absoluto de 1 cm al medir la longitud de una
carretera que al medir la longitud de un folio.
El error absoluto es el
valor absoluto de la diferencia entre el valor exacto y el valor aproximado.
EA
= | P* - P |
4.5.- Error relativo
El error relativo es el
cometido en la estimación del valor de un número, es el valor absoluto del
cociente entre su error absoluto y el valor exacto. El error relativo da idea
de la precisión de una medida, y se suele manejar en forma de porcentaje (%).
Muchas veces conocemos el
error absoluto (EA), pero es imposible conocer el valor exacto (A), en cuyo
caso, para hallar el error relativo (ER) dividimos el error absoluto entre el
valor aproximado o considerado como exacto.
ER =
(| P* - P| )/ P , si P =/ 0
4.6.- Error porcentual
Es el resultado de multiplicar el error relativo por 100
y se expresa en porcentaje (%).
ERP =
ER x 100
Ejemplo
de los errores absoluto, relativo y porcentual:
Supóngase que se tiene que
medir la longitud de un puente y de un remache, obteniéndose 9 999 y 9 cm,
respectivamente. Si los valores son 10 000 y 10 cm, calcúlese a) el error y b)
el error relativo porcentual de cada caso.
a): El
error de medición del puente es:
EA = 10 000 - 9 999 = 1cm
y para el remache es de
EA = 10 - 9 = 1cm
b) El error relativo porcentual para
el puente es de:
ERP = 1/ 10 000 x 100% = 0.01%
y para el remache es de
ERP = 1/10 x 100% = 10%
5.- CONVERGENCIA
Se dice que hay “Convergencia” al utilizar un método numérico
para resolver un problema en particular cuando, mientras más iteraciones se
hacen se obtiene una mejor aproximación al resultado.
En Métodos numérico la velocidad
con la cual una sucesión converge a su límite es llamada orden de convergencia. Este
concepto es, desde el punto de vista práctico, muy importante si necesitamos
trabajar con secuencias de sucesivas aproximaciones de un método iterativo. Incluso puede hacer la diferencia entre necesitar diez o un
millón de iteraciones.
6.- PROGRAMAS COMPUTACIONALES
Entre los programas más usados en los métodos numéricos
se encuentran:
6.1.- WxMáxima
Wxmaxima es una potente
herramienta para cálculos matemáticos para el estudio de funciones, polinomios,
permite realizar cálculos algebraicos. Se pueden graficar funciones en forma 2D
y 3D, especificando los límites de los ejes, graduación de la escala, etc.
6.2.- Patran
Es un programa de ingeniería asistida por computadora que proporciona una interfaz gráficaal pre y pos-procesado de modelo de elementos finitos y sus procesados.
Patran proporciona un rico
conjunto de herramientas que simplifican la
creación de modelos de análisis listos para lineal, dinámica, no lineal, explícito, térmicas y otros solucionado de elementos finitos.
6.3.- Integralab
Sirve como una herramienta para
resolver problemas de integración de funciones y solución de ecuaciones
diferenciales ordinarias aplicando métodos numéricos. El software ha sido
probado en cuanto a sus resultados tomando funciones cuyos resultados son
conocidos y presentados en la literatura sobre métodos numéricos y luego
contrastados con los obtenidos o devueltos por IntegraLAB, encontrado precisión
y exactitud en conformidad con los resultados esperados.
6.4.- Elmer
Es un programa para la solución de problemas de
elementos finitos. Un software de
código abierto de simulación desarrollado por multiphysical. Los modelos
físicos de la dinámica de fluidos, mecánica estructural, electromagnetismo, transferencia
de calor y la acústica. Estos
son descritos por ecuaciones diferenciales
parciales que Elmer resuelve por el método de elementos finitos.
6.5.- Octave
Es un programa y lenguaje de programación para realizar cálculos numéricos.
·
Octave
está escrito en C++ usando
la biblioteca STL.
·
Tiene un
intérprete de su propio lenguaje (de sintaxis casi idéntica a Matlab), y
permite una ejecución interactiva o por lote.
·
Su
lenguaje puede ser extendido con funciones y procedimientos,
por medio de módulos dinámicos.
·
Utiliza
otros programas GNU para
ofrecer al usuario la posibilidad de crear gráficos para luego imprimirlos o
guardarlos (Grace).
7.- CONCLUSIÓN
Los métodos numéricos son herramientas poderosas,
capaces de manejar sistemas de ecuaciones grandes y complicadas que son difíciles
de resolver analíticamente.
Podemos darnos cuenta que los métodos numéricos pueden
aplicarse en distintos campos para encontrar los resultados aproximados a
sistemas complejos utilizando solo las operaciones matemáticas más simples. Es
importante conocer los métodos numéricos para facilitarnos la resolución de
problemas matemáticos que tienen múltiples aplicaciones en la vida real, además
de que nos permite resolver problemas con mayor eficiencia, es por ello que es
preciso manejar modelos que faciliten a resolución de estos.
8.- BIBLIOGRAFÍA
http://www.monografias.com/trabajos98/metodo-numerico/metodo-numerico.shtml
https://www.varsitytutors.com/hotmath/hotmath_help/spanish/topics/taylor-series
https://sites.google.com/site/metalnumericos/home/unidad-1/1-2-tipos-de-errores-error-absoluto-error-relativo-error-porcentual-errores-de-redondeo-y-truncamiento
https://sites.google.com/site/metnum00/home/unidad-i/1-2-tipos-de-errores
http://test.cua.uam.mx/MN/definiciones.php
http://correo.uan.edu.mx/~iavalos/FP/FP1.html
https://definicion.de/aproximacion/
http://www.monografias.com/trabajos12/moma/moma.shtml
https://www.geogebra.org/m/n9bpyzdw


No hay comentarios:
Publicar un comentario