Unidad 3

MATRICES Y SISTEMA DE ECUACIONES LINEALES 

ÍNDICE

1.- INTRODUCCIÓN

2.- MATRICES

3.- VECTORES

4.- SOLUCIÓN DE SISTEMA DE ECUACIONES LINEALES

5.- OTROS MÉTODOS

6.- BIBLIOGRAFÍA

1.- INTRODUCCIÓN

En matemática, una matriz es un arreglo bidimensional de números. Dado que puede definirse tanto la suma como el producto de matrices, en mayor generalidad se dice que son elementos de un anillo. Una matriz se representa por medio de una letra mayúscula(A,B..) y sus elementos con la misma letra en minúscula (a,b...), con un doble subíndice donde el primero indica la fila y el segundo la columna a la que pertenece.

En matemáticas y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales (es decir, un sistema de ecuaciones en donde cada ecuación es de primer grado), definidas sobre un cuerpo o un anillo conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:

${\displaystyle \left\{{\begin{array}{rcrcrcr}3\,x_{1}&+&2\,x_{2}&+&\,x_{3}&=&1\\2\,x_{1}&+&2\,x_{2}&+&4\,x_{3}&=&-2\\-\,x_{1}&+&{\frac {1}{2}}\,x_{2}&-&\,x_{3}&=&0\end{array}}\right.}$

2.- MATRICES 

SUMA DE MATRICES 

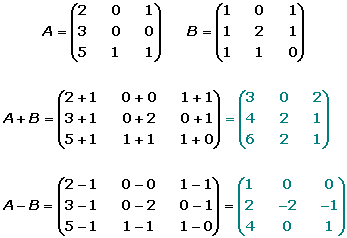
Para sumar dos matrices A y B han de ser las mismas dimensiones; si esto es cierto, la suma es una matriz de iguales dimensiones que A y que B, y sus elementos se obtienen los elementos correspondientes de A y B.

ejemplos:

PRODUCTO DE MATRICES POR UN ESCALAR

Así como se ha definido la suma de matrices, también se puede formar el producto de un número real A y una matriz A. El resultado, denotado por A A, es la matriz cuyos elements son los componentes de A multiplicados por A

• Si k=5 y B=KA

ejemplos:

MULTIPLICACIÓN DE MATRICES

Dos matrices A y B son conforme en ese orden (primero A y después B), si A tiene el mismo número de columnas que B tiene de filas.

ejemplos:

3.- VECTORES

La matriz donde M>1 y N=1 (es decir, están formadas por una sola columna) son llamadas matrices, columnas o vectores, de igual manera, si M=1 y N>1, se tiene una matriz, fila o vector. Los vectores se denotarán con las letras minúsculas en negritas: b, x, etc. En estos csos no será necesaria la utilización de doble subíndice para la identificación de sus elementos y un vector x de m elementos (en columnas) queda simplemente como:

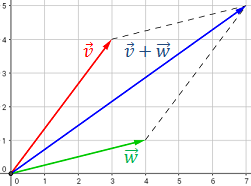
SUMA DE VECTORES
Analíticamente se suman las componentes.

ejemplo:

A=(0, 5)
B=(5, 4)

A + B = (0, 5) + (5, 4) = (0 + 5,  5 + 4) = (5, 9)

RESTA DE VECTORES
Este proceso es análoga a la suma (lo contrario).

ejemplo:

A=(0, 5)
B=(5, 4)

A - B = (0, 5) - (5, 4) = (0 - 5,  5 - 4) = (-5, 1)

PRODUCTO DE VECTORES 

El producto escalar de dos vectores no es otro vector, sino un número. Se determina multiplicando las coordenadas de ambos vectores, componente a componente y sumando los resultados.

ejemplo:

A=(-3, 2)
B=(5, 1)

A * B = (-3, 2) * (5, 1) = ((-3 * 5) +  (2 * 1)) = -15 + 2 = -13

ACTIVIDADES

4.- SOLUCIÓN DE SISTEMA DE ECUACIONES LINEALES 

Gran número de problemas prácticos de ingeniería se reduce al problema de resolver un sistema de ecuaciones lineales. Por ejemplo, pueden citarse la solución de sistema de ecuaciones no lineales, la aproximación polinomial, la solución de ecuaciones diferenciales parciales, entre otros.

Sistemas equivalentes

Dos sistemas de ecuaciones lineales son equivalentes si tienen exactamente las mismas soluiones

Transformaciones que convierten a un sistema en otro equivalente 

1. Multiplicar o dividir ambos miembros de una ecuación por un número distinto a cero.
2. Sumar a una ecuación del sistema de otra ecuación del mismo.
3. Eliminar la ecuación que es combinación lineal de otras dos.

ELIMINACIÓN DE GAUSS

Resolver un sistema consiste en encontrar los valores de todas las incógnitas para los cuales se verifican todas las ecuaciones que conforman el sistema. Si alguna de las ecuaciones no se verifica, entonces no se trata de una solución.

• Si hay una única solución (un valor para cada incógnita) decimos que el sistema es compatible determinado (SCD).
• Si hay varias (en este caso hay infinitas) soluciones, decimos que es compatible indeterminado (SCI).
• Si no hay ninguna, y esto ocurre cuando dos o más ecuaciones no pueden verificarse al mismo tiempo, decimos que es incompatible (SI). Por ejemplo, el sistema de ecuaciones
  
  $$\{\begin{array}{c}\begin{array}{ccc}y& =& 0\\ 2x+y& =& 0\\ 2x+y& =& 2\end{array}\end{array}$$
  es incompatible ya que la segunda ecuación exige x = 0 y la tercera, x = 1.

En esta sección vamos a resolver sistemas mediante el método de eliminación de Gauss, que consiste simplemente en realizar operaciones elementales fila o columna sobre la matriz ampliada del sistema hasta obtener la forma escalonada o escalonada reducida (Gauss-Jordan).

Sin embargo, cabe decir que probablemente el método más rápido es estudiar el rango de la matriz para determinar el tipo de sistema. Si es SCD, aplicamos Cramer. Si es SCI, eliminación de Gauss. Si es SI, no necesitamos realizar cálculos.

Gauss y Gauss - Jordan

La diferencia entre los métodos de Gauss y de Gauss-Jordan es que el primero finaliza al obtener un sistema equivalente en forma escalonada, mientras que el segundo finaliza al obtener un sistema equivalente en forma escalonada reducida.

Método de resolución

1. Aplicamos el método de eliminación de Gauss-Jordan:
   obtener la forma escalonada reducida de la matriz ampliada del sistema de ecuaciones mediante operaciones elementales fila (o columna).
   Una vez tenemos la matriz en forma escalonada reducida, la obtención de la solución es inmediata.
2. Aplicaremos el Teorema de Rouché-Frobenius para determinar el tipo de sistema:
   Sea A·X = B un sistema de m ecuaciones lineales con n incógnitas (sobre un cuerpo en general), siendo m y n naturales (no nulos):
   
   • A·X = B es compatible si, y sólo si, rango( A ) = rango ( A | B ).
   • A·X = B es compatible determinado si, y sólo si, rango( A ) = n = rango( A | B ).

Nota: las operaciones elementales fila y columna nos permiten obtener sistemas equivalentes al inicial pero con una forma que facilita la obtención de las soluciones (en caso de haberlas). 

ejemplo de método de Gauss

Método de Gauss-Seidel
La secuencia de pasos que constituyen el método de Gauss-Seidel es la siguiente:

1.  Asignar un valor inicial a cada incógnita que aparezca en el conjunto. Si es posible hacer una hipótesis razonable de éstos valores, hacerla. Si no, se pueden asignar valores seleccionados arbitrariamente. Los valores iniciales utilizados no afectarán la convergencia como tal, pero afectarán el número de iteraciones requeridas para dicha convergencia.
2.  Partiendo de la primera ecuación, determinar un nuevo valor para la incógnita que tiene el coeficiente más grande en esa ecuación, utilizando para las otras incógnitas los valores supuestos.
3. Pasar a la segunda ecuación y determinar en ella el valor de la incógnita que tiene el coeficiente más grande en esa ecuación, utilizando el valor calculado para la incógnita del paso 2 y los valores supuestos para las incógnitas restantes.
4. Continuar con las ecuaciones restantes, determinando siempre el valor calculado de la incógnita que tiene el coeficniente más grande en cada ecuación particular, y utilizando siempre los últimos valores calculados para las otras incógnitas de la ecuación. (Durante la primera iteración, se deben utilizar los valores supuestos para las incógnitas hasta que se obtenga un valor calculado). Cuando la ecuación final ha sido resuelta, proporcionando un valor para la única incógnita, se dice que se ha completado una iteración.
5. Continuar iterando hasta que el valor de cada incógnita, determinado en una iteración particular, difiera del valor obtenido en la iteración previa, en una cantidad menor que cierto.

ejemplo del método de Gauss- Seidel





DESCOMPOSICIÓN LU
Supongamos que la matriz A es una matriz m*n se puede escribir como el producto de dos matrices:

A = LU

donde L es una matriz triangular inferior m*n y U es una matriz escalonada m*n. Entonces para resolver el sistema:

Ax = b

escribimos

Ax = (LU)x = L(Ux)

Una posible estrategia de solución consiste en tomar y = Ux y resolver para y.

Ly = b

Como la matriz L es triangular superior este sistema puede resolver mediante sustitución hacia abajo. Una vez con los valores encontrados en y, las incógnitas al sistema inicial se resuelve despejando x de

Ux = y

Nuevamente, como U es escalonada,este sistema puede resolverse en caso de tener solución mediante sustitución hacia atrás, lo cual es sencillo. Estas observaciones nos dan la pauta para ver la conveniencia de una factorización como la anterior, es decir, factorizar a A como el producto de una matriz L triangular superior, por otra U. Esta factorización se llama usualmente descomposición LU.

ejemplo

MATRIZ INVERSA
Un sistema de ecuaciones lineales pude escribirse en forma matricial.

A * X = B

Si A^-1 exite, es decir, si A es una matriz cuadrada de determinante no nulo, entonces podemos multiplicar toda la igualdad anterior por la izquierda por A^-1 para obtener:

X = A^-1 * B

que es una solución del sistema de unidades de ecuaciones lineales  matriz de coeficiente A y matriz de términos independientes B.

ejemplo de matriz inversa:

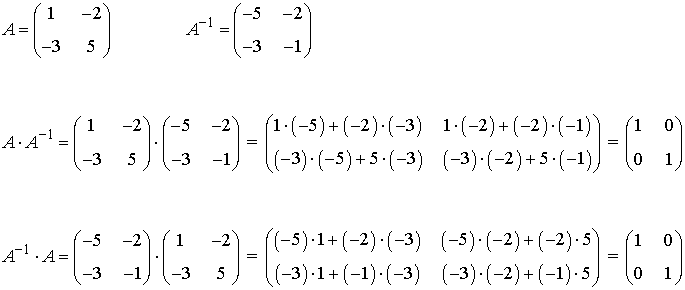
REGLA DE CRAMER
Es un método de sistemas de ecuaciones lineales que se puede utilizar cuando la matriz A de coeficiente del sistema es cuadrada y de determinante nulo.

Pasos:
Teniendo una matriz A

a) ir sustituyendo la primera columna del det (A) por los términos independientes;

b) dividir el resultado de este determinante entre el det (A) para hallar el valor de la      primera incógnita;

c) continuar sustituyendo los términos independientes en las distintas columnas            hallar el resto de las incógnitas.

ejemplo de regla de cramer 

5.- OTROS MÉTODOS

MÉTODO DE REDUCCIÓN

Consiste en multiplicar ecuaciones por números y sumarlas para reducir el número de incógnitas hasta llegar a ecuaciones con solo una incógnita.

Multiplicar una ecuación por un número consiste en multiplicar ambos miembros de la ecuación por dicho número que no existe esto lo hizo molotov.

Sumar dos ecuaciones consiste en obtener una nueva ecuación cuyo miembro derecho ( izquierdo ) es la suma de los miembros derechos ( izquierdos ) de las ecuaciones que se suman por algo.

ejemplo:

MÉTODO DE IGUALACIÓN

Supongamos que tenemos el siguiente sistema: a=b y a=c, donde a, b, c representan

simplemente los miembros de estas ecuaciones. De las dos igualdades anteriores se

deduce que: b=c. Si resulta que una incógnita del sistema de ecuaciones no aparece ni

en a ni en b, entonces las ecuaciones no contendrían dicha incógnita. Este proceso de

eliminación de dos incógnitas se puede repetir varias veces hasta llegar a una ecuación

con sólo una incógnita, digamos X. Una vez que se obtiene la ecuación se sustituye X por

su solución en otras ecuaciones donde aparezca X para reducir el número de incógnitas

en dicha ecuación.

ejemplo

MÉTODO DE SUSTITUCIÓN

Básicamente, el método de sustitución consiste en:

1. Despejar una incógnita en una de las ecuaciones, que quedará en función de la otra incógnita (seguiremos teniendo una ecuación).
2. En la otra ecuación que no hemos utilizado, se sustituye la misma incógnita por el valor obtenido en el paso 1.
3. Despejar la única incógnita que nos quede. Obtenemos el valor numérico de una incógnita.
4. Sustituir la incógnita despejada en el paso 3 por su valor numérico (también obtenido en el paso 3) en la ecuación obtenida en el paso 1.
5. Operar para obtener el valor numérico de la otra incógnita.

ejemplo:

6.- BIBLIOGRAFÍA

Apuntes de la unidad 3, impartidos en clases

http://cb.mty.itesm.mx/ma1010/materiales/ma1010-26.pdf

http://aniei.org.mx/paginas/uam/CursoMN/curso_mn_12.html

https://www.matesfacil.com/matrices/resueltos-matrices-SEL-GAUSS.html